This is one of over 2,200 courses on OCW. Find materials for this course in the pages linked along the left. MIT OpenCourseWare is a free & open publication of material from thousands of MIT courses, covering the entire MIT curriculum. No enrollment or registration. Freely browse and use OCW materials at your own pace. There's no signup, and no start or end dates.

Knowledge is your reward. Use OCW to guide your own life-long learning, or to teach others. We don't offer credit or certification for using OCW.

Made for sharing. Download files for later. Send to friends and colleagues. Modify, remix, and reuse (just remember to cite OCW as the source.) Learn more.

Fourier Representation of continuous time signals. Representing a signal in terms of its exponential Fourier series components is called Fourier Analysis. Fourier Series & Fourier Transforms nicholas.harrison@imperial.ac.uk 19th October 2003 Synopsis Lecture 1: • Review of trigonometric identities.

• The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To make a donation or view additional materials from hundreds of MIT courses, visit MITOpenCourseWare@OCW.MIT.edu.

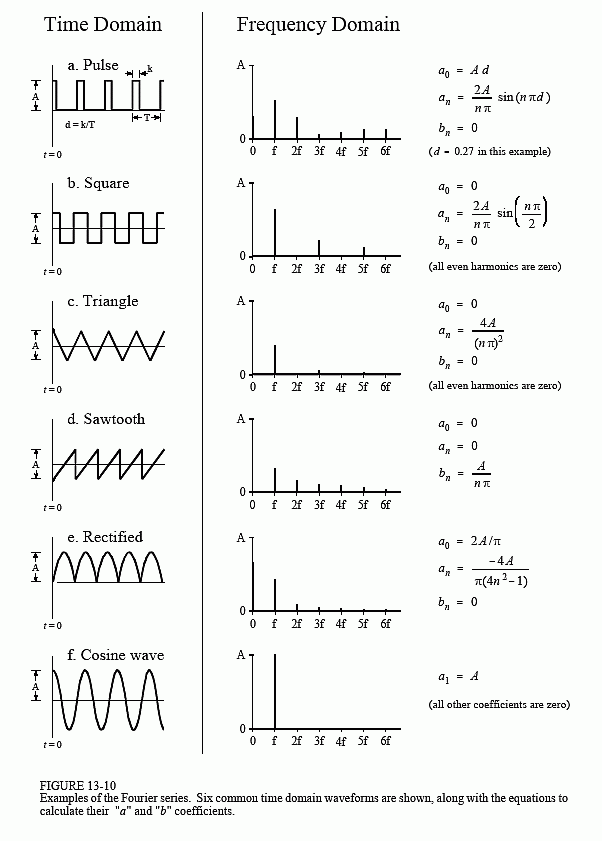
PROFESSOR: Welcome. One quick announcement-- if you have not yet picked up your graded exams, you can do so by seeing the TAs after the hour. So today I want to continue to think about what we started last week, thinking about Fourier series. The idea is to develop a theory that lets us look at signals on the basis of frequency content, much as we looked at frequency responses as a characterization of systems, according to the way they process frequencies. And we saw last time that there were a number of kinds of signals, for example, musical signals, where that kind of an on approach-- thinking about the signal according to the frequencies that are in it-- makes a lot of sense and can lead to insight.

We also developed some formalism. We figured out how you can break a signal into components and then assemble the components to generate the signal.

And what I want to mention at the beginning of the hour today is just how to think about this operation in a more familiar way. We do this kind of a thing, breaking something into components all the time. One of the more familiar examples might be thinking about 3-space, right? The Cartesian analysis of 3-space is based on the idea that you can think about a vector location in 3-space as having components.

There's a component in the x direction, the y direction, the z direction. That's completely analogous to the way we're thinking about Fourier representations for signals. Web R New Version For Pc more. So just like we would think about synthesizing the location of a point by adding together three pieces, and we would think about analyzing a point to figure out how big the components are in each of those directions, it's exactly the same when we think about Fourier series.

We think about representing a signal as a sum of things. So the sum is precisely the same. This one happens to have an infinite number of terms, [? Eh.?] The top one has three terms, [? Eh.?] The principles are very similar.

So we think about representing a signal as a sum of components. We think about representing a point in 3-space as a sum of components, and we think about analyzing the signal or the vector in 3-space, so that we figure out what each of those components are. And we do it in an operation where it's actually very convenient to think about the decomposition of the Fourier components using precisely the same language that we would use for thinking about vector spaces. So we would think about-- in the case of the Fourier, we think about integrating over the period sifts out a component.

The analogous operation for 3-space is to think about a dot product. The way you take a vector and figure out the component in the x direction is to dot it with it, the dot product. In the Fourier case, we think about it as being an inner product. The idea is completely analogous. So we think about having the inner product of two things-- the reference direction and the vector.